Self-Similar Structure in an Exchangeable Model for Population Dynamics

Joshua Speckman (USC), Ruoyu Lin (U of Boston)

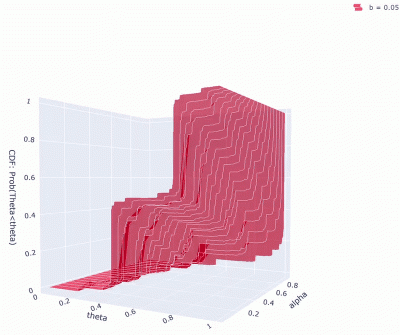
In this work we study a model for biological evolution that exhibits both exchangeability and self-similarity. The model considers an infinite sequence of sites which are subject to an environment, modeled by a two-state Markov chain. Each site has a unique fitness value which is updated at discrete time units according to the environment and its own “luck”. We established the long-term behavior of the model and obtained an explicit expression for the limit self-similar distribution. Specifically, the empirical fitness distribution converges a.s.  to some random limiting distribution, which we were able to explicitly identify. The image below shows some of these distributions. The axis  labeled by $\theta$ represents the distribution of the proportion of the population under some fixed fitness value. The axis labeled by $\alpha$ represents one diagonal value of the transition matrix, and the images differ in the other diagonal value of the transition matrix.

 

Maximal Couplings for Finite State Markov Chains

Jack Hanke (UCONN), Aenea Ferguson (Withmore College)

We continued a research line from last year and  worked on explicit constructions for maximal coupling and properties of maximal couplings, such as uniqueness (under reasonable assumptions) or being Markovian. Our main results provide a simple algorithm for the construction of  a maximal coupling, a result which can be deferred from existing and more general results, and an investigation of uniqueness of the distributions of the marginal processes under some conditions on the coupling.

Quasistationary Distributions for the Invasion and Voter model

Van Hovenga (U of Colorado, Colorado Springs), Edith Lee (U of Michigan)

In this project we  examined QSDs for a more general class of interacting particle systems than those studied last year. Our specific focus was on the invasion model, where unlike the voter model on complete bipartite graphs, this induces high-level of disorder and which turns out to be a harder model to study. Our work focused on the following aspects:

• Simulation of the QSD. This is a non trivial problem because we’re trying use find probabilities obtained by conditioning on events with geometrically vanishing probabilities.
• Numerical calculation of the QSD.
• Rigorous study of the rate of convergence to consensus. Unlike the voter model that has a closed-form formula for this quantity,  here we had to resort to perturbation theory for nonnegative matrices.

This work was continued and completed in MCREU `21.