This page is being updated…
An Implementation of a Maximal Coupling Algorithm for Markov Chains
Alan Boles (University of Tennessee, Knoxville), Leila Dahlia (Univerity of Illinois, Chicago), Scott McIntyre (University of California, Berkley), Bronson Zhou (University of Texas, Austin)
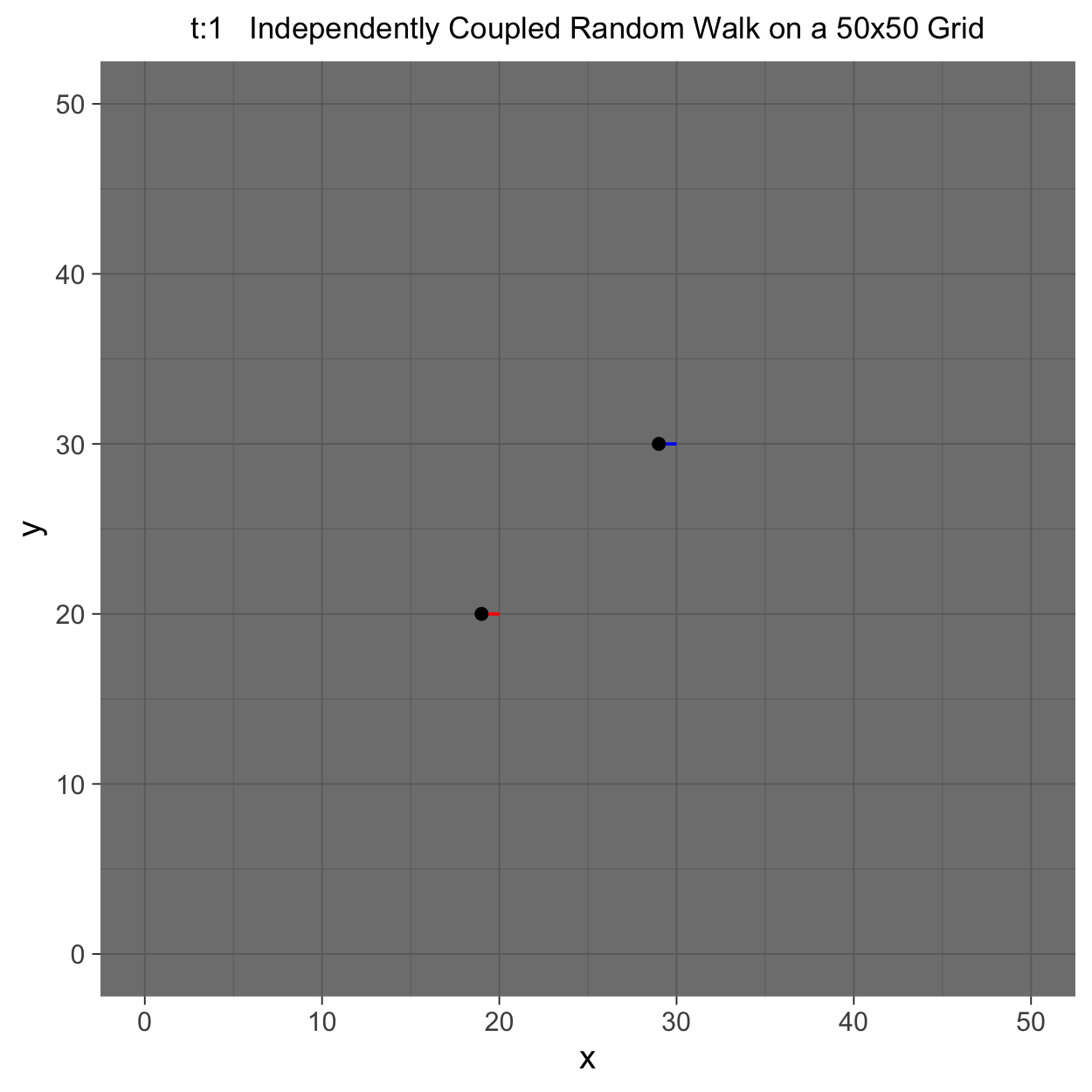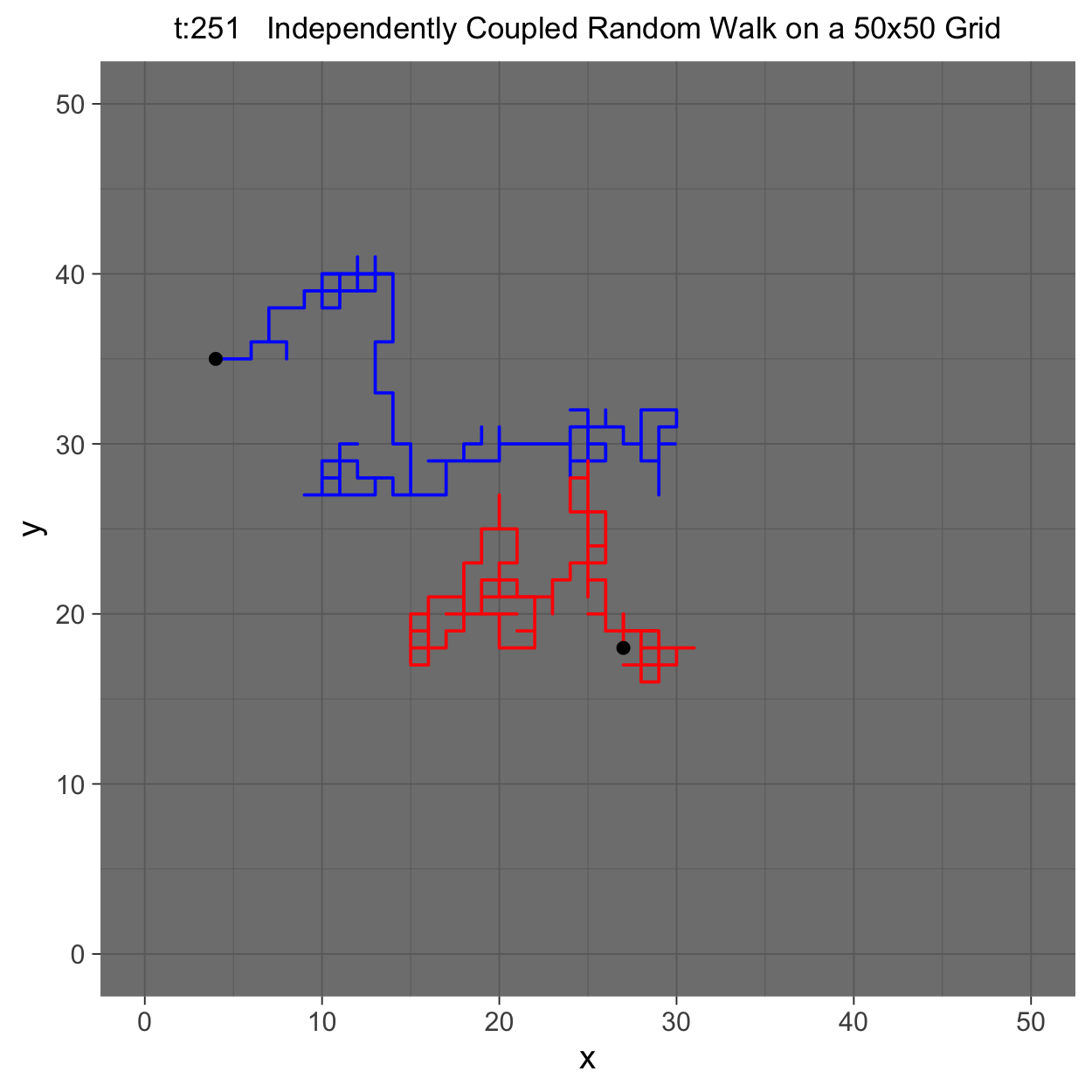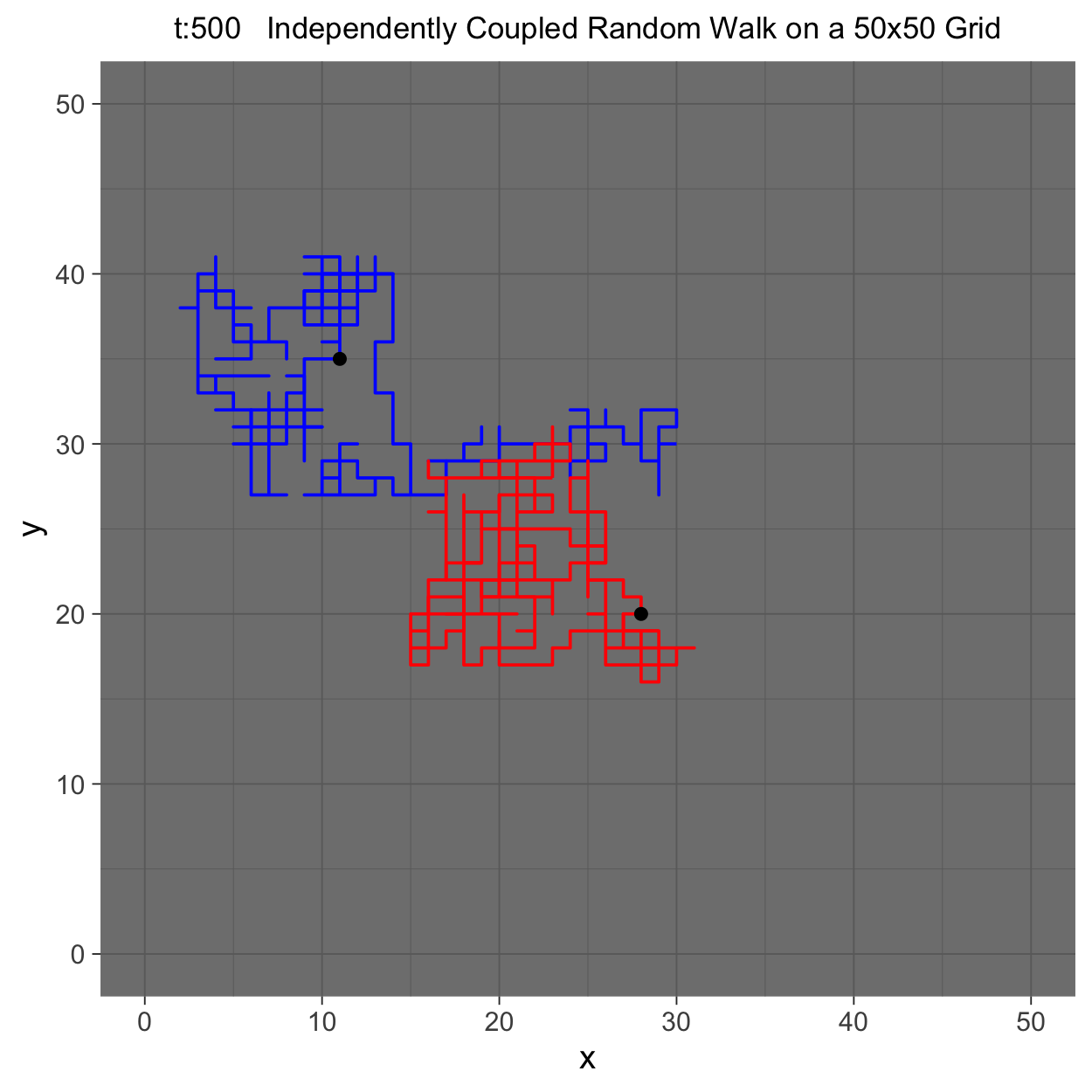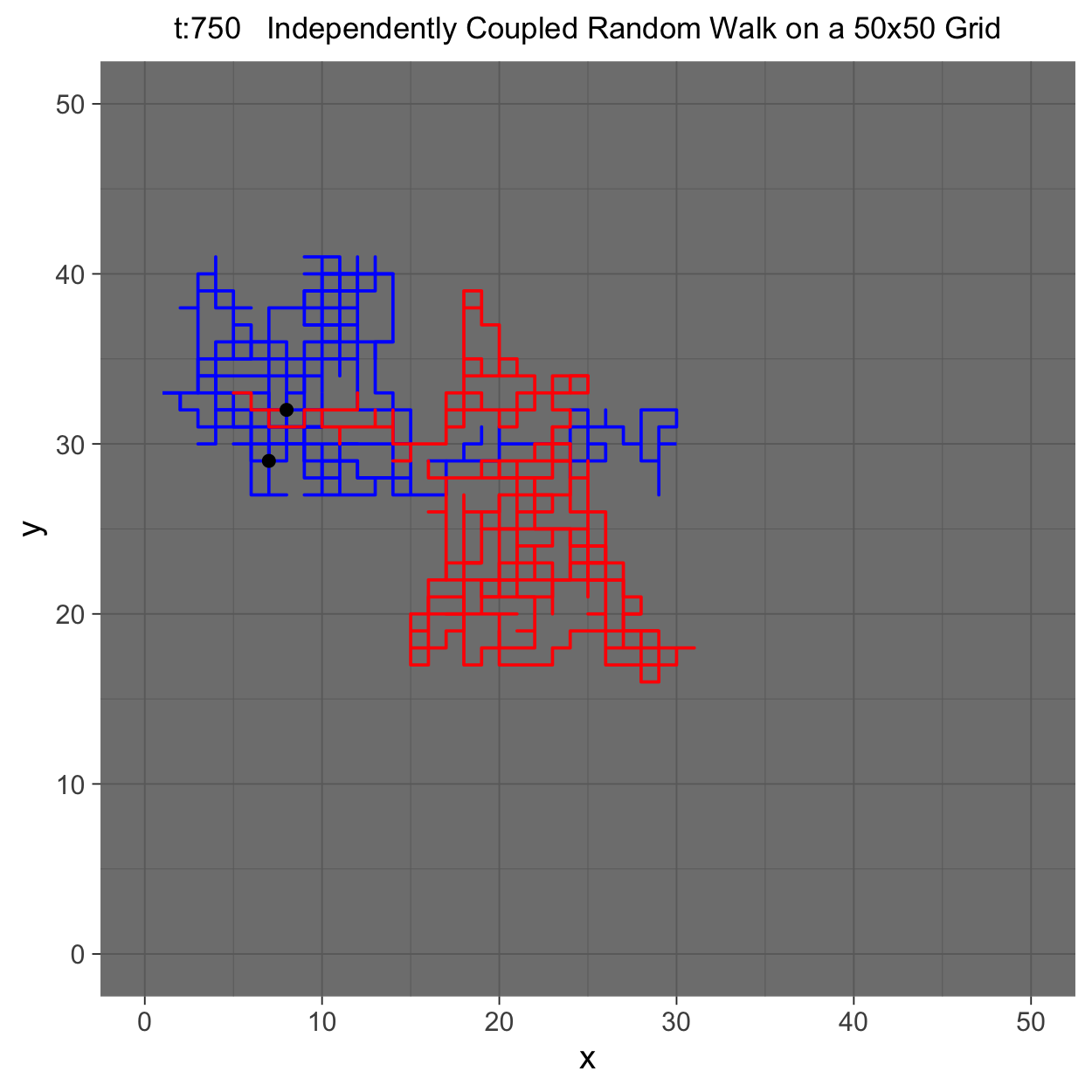
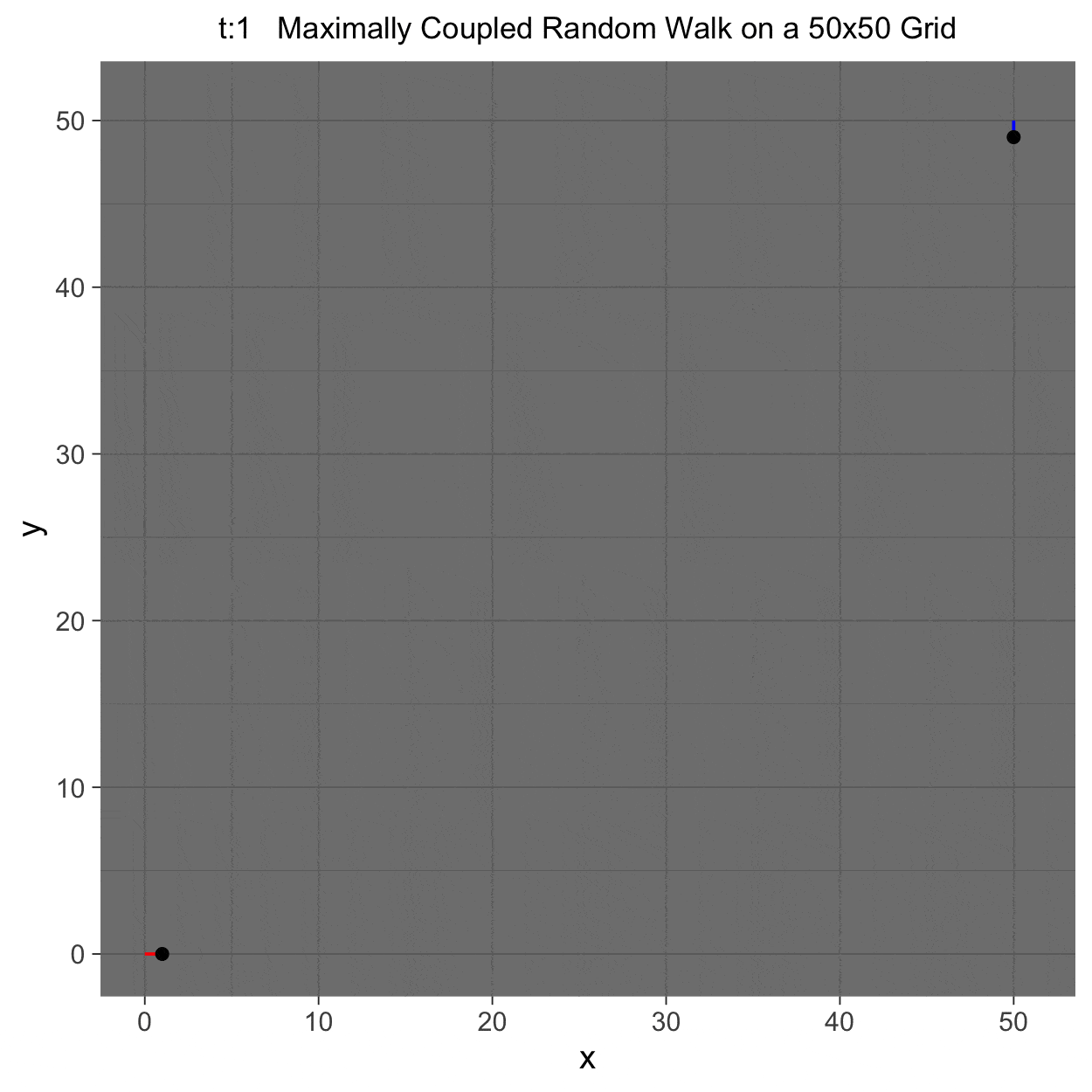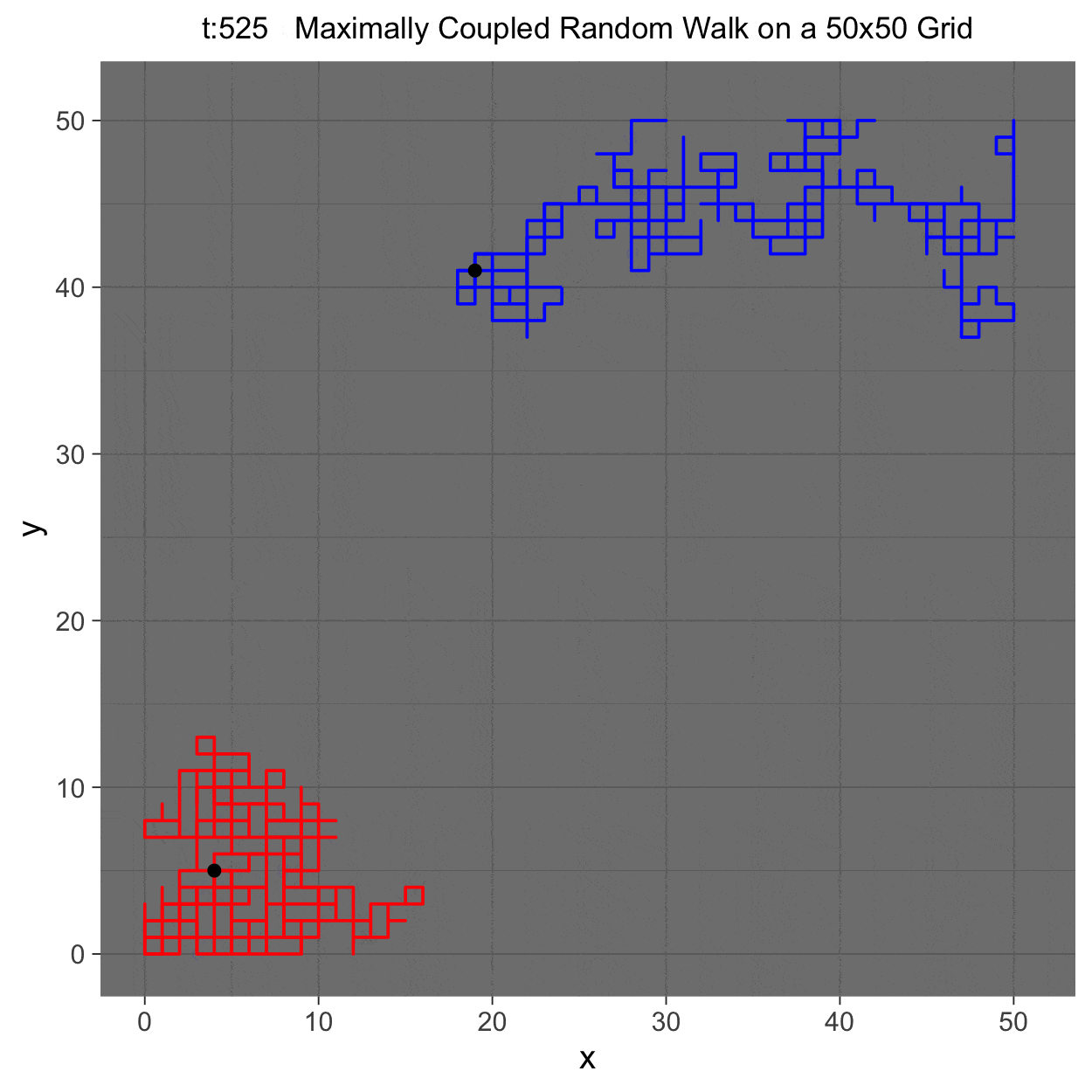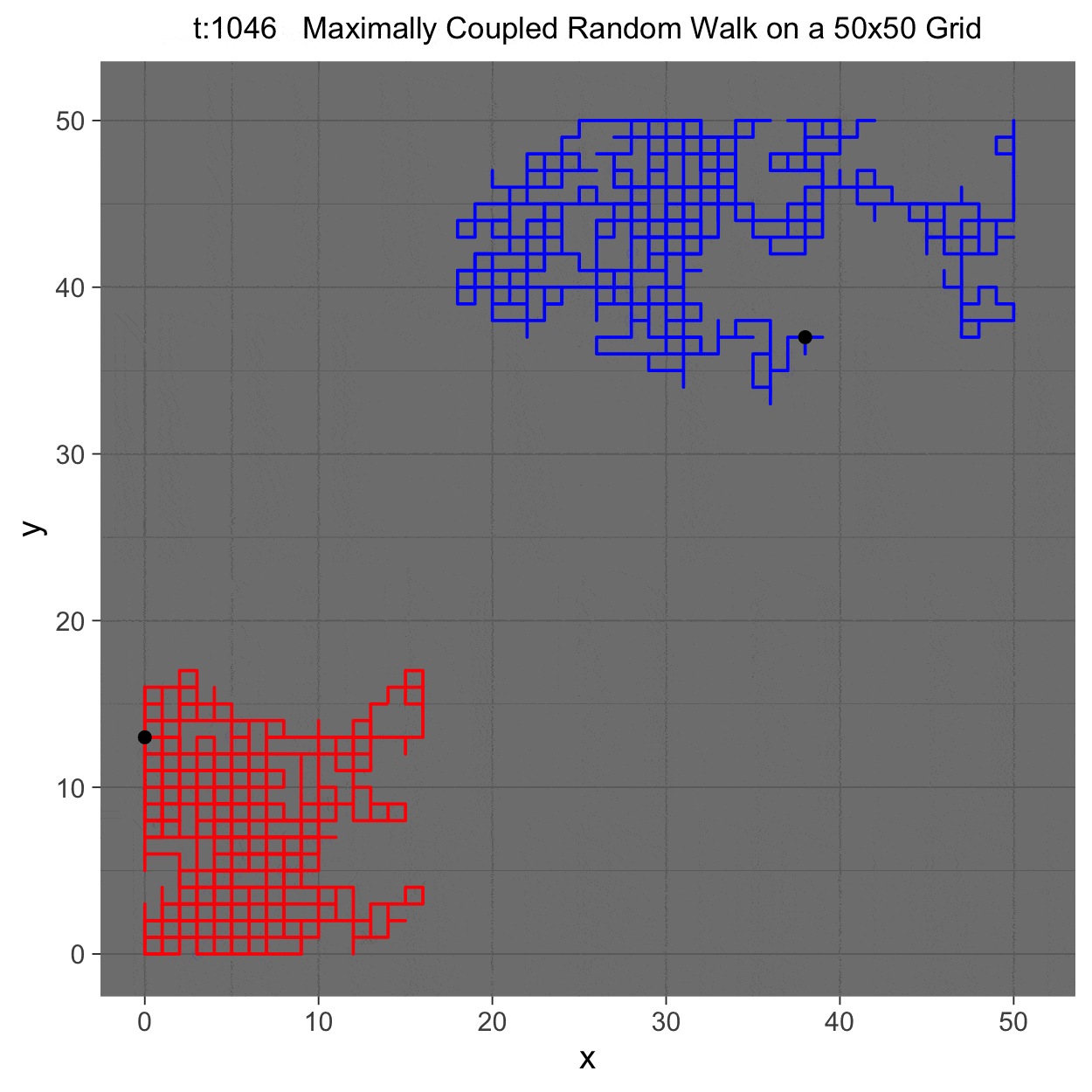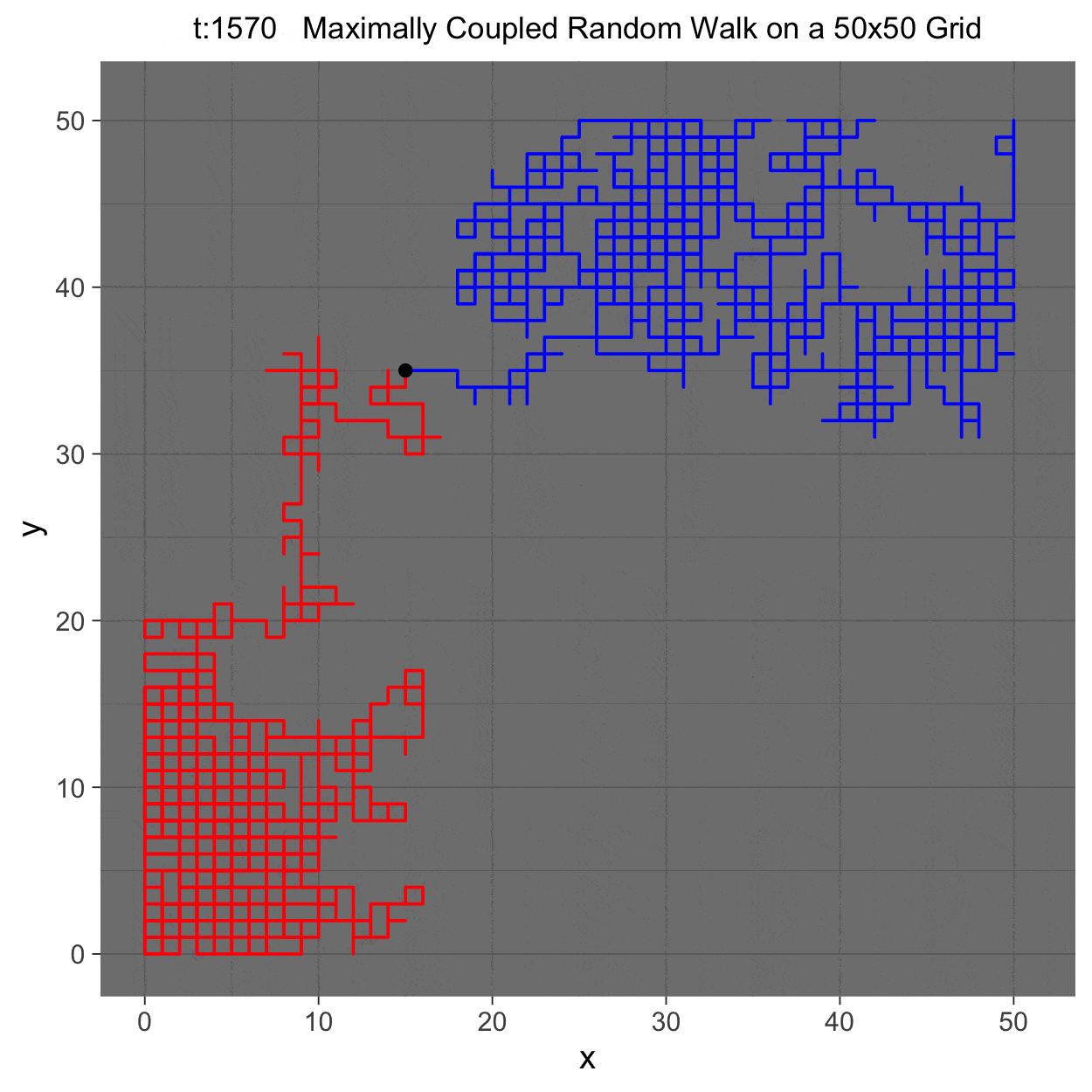
This project gleans insights surrounding maximal couplings initialized by Griffeath 1975 and Pitman 1976, looking toward building a general algorithm for maximal coupling. Our exploration began with a simple random walk on a cycle, understanding the work of Pitman, implementing an algorithm for sampling maximal couplings via path decomposition, and, finally, observing the coupling behavior of random walks in \(\mathbb{Z}^{2}\). In our approach to maximal couplings, we restricted our approach to finite state discrete Markov processes. Looking further, we aim to implement this approach to infinite state discrete time Markov processes toward building a general purpose maximal coupling package in Julia with visualization recipes, along with polishing the implementation written in R which produced the graphics shown below, which depict a random walk on \(\mathbb{Z}^{2}\)
Sampling Minimal Quasi-Stationary Distributions through a Renewal Formula
Gabe Cantanelli (U Texas, Arlington), Elza Moore (Scripps College)
Our project centers around the implementation and performance evaluation of a novel method for sampling the minimal quasi-stationary distribution of a Markov Chain based upon a renewal formula. We implemented the method specifically using subcritical Galton-Watson branching processes with various offspring distributions, and implemented it in both Python and R. We also investigated the performance of the method in relation to different renewal rules. As a result of our work, we aim to produce working Python and R packages capable of estimating QSDs using our formula, as well as visualizing them graphically.
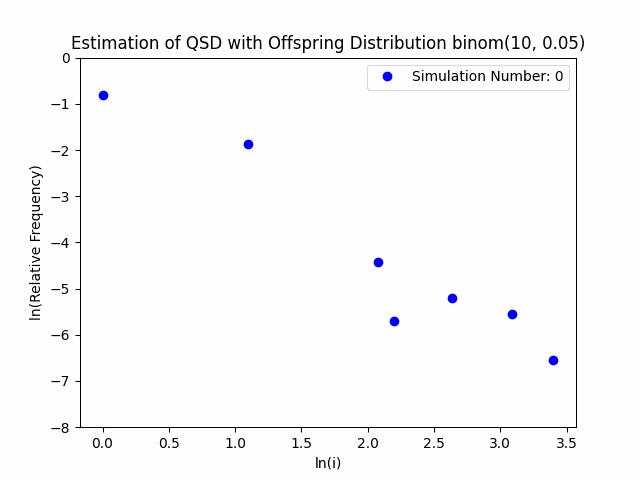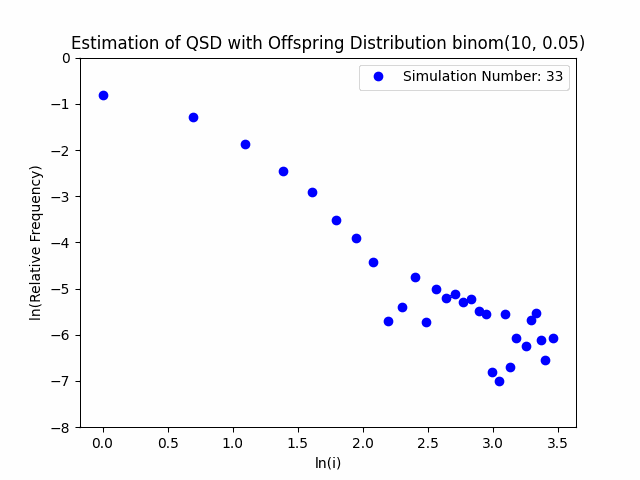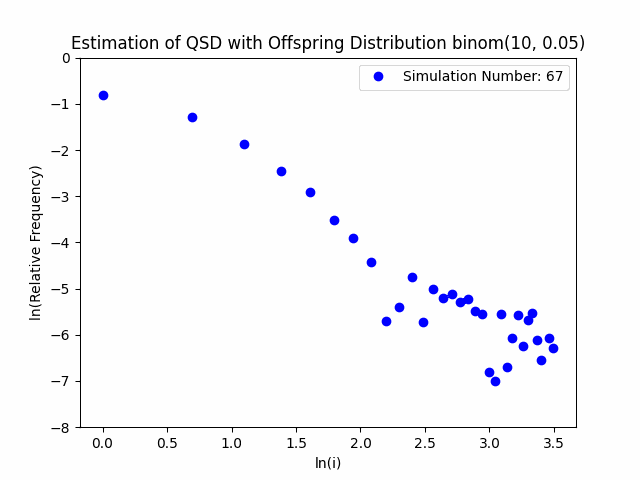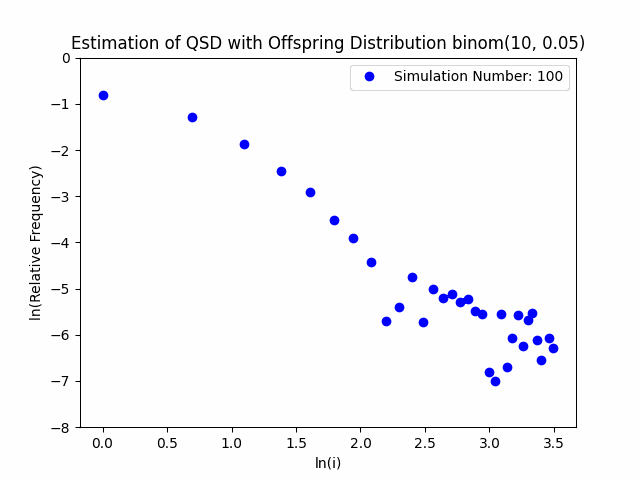
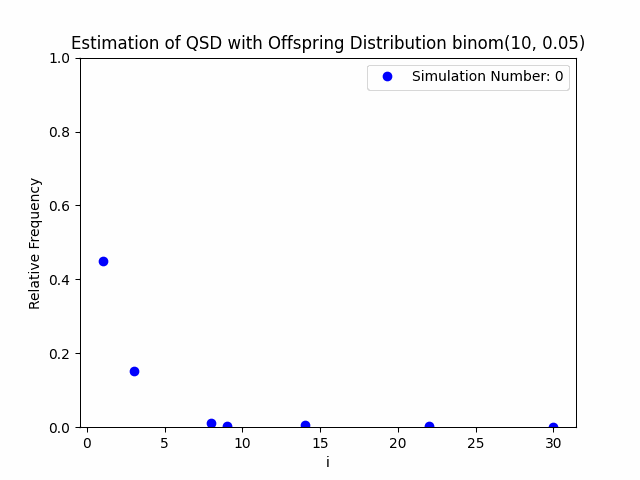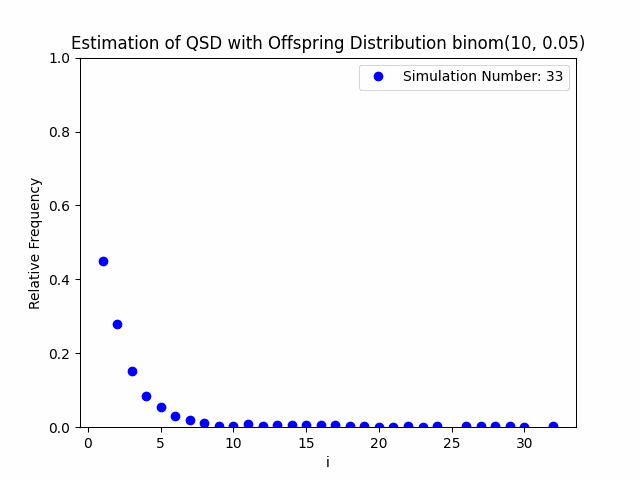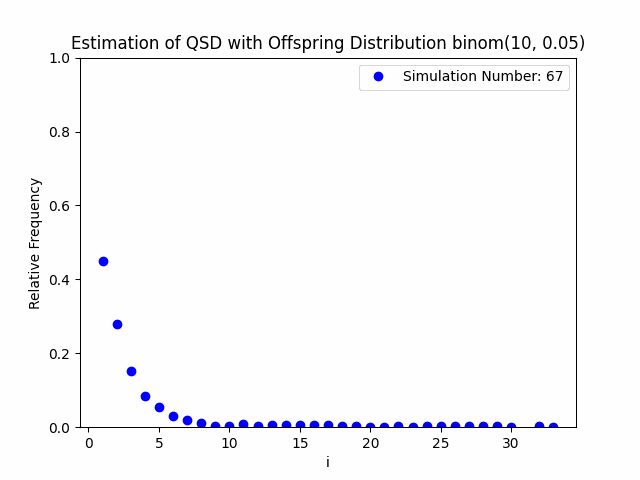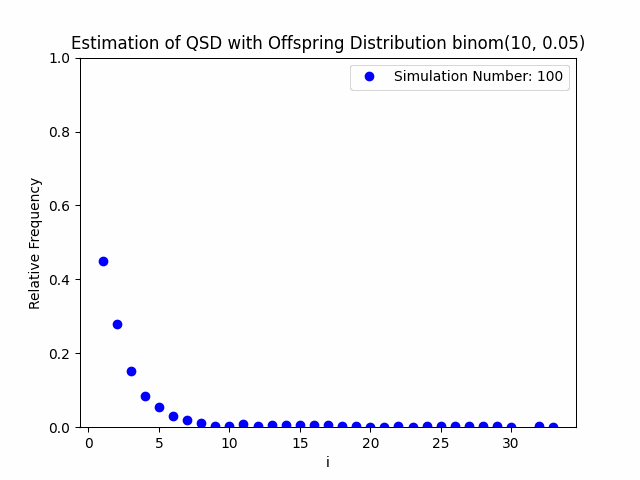
In addition to our approach, we also implemented different probabilistic and numerical methods for sampling QSDs from the literature in order to compare them to ours. Such methods include another renewal-based approach and a recursion-interpolation scheme, as discussed within the paper on low-rank sampling by Hautphenne and Massei (2020).
Coalescing Random Walks
Bram Silbert (Wesleyan U), Lillian (Ian) Makhoul (Lehigh University)
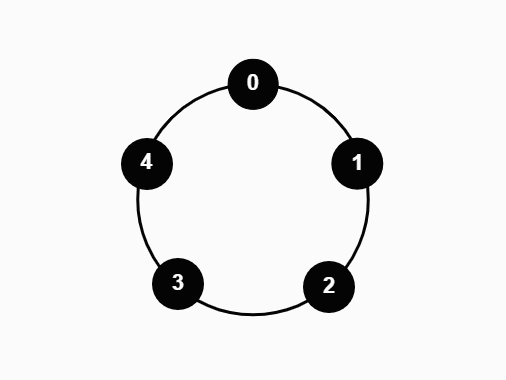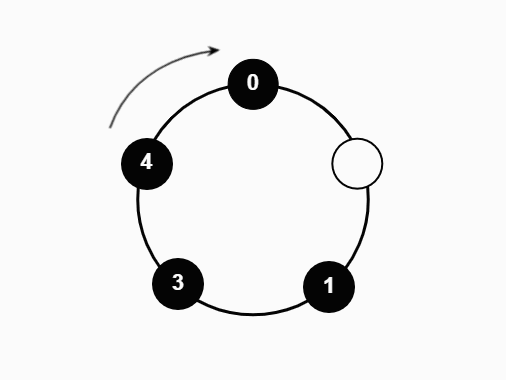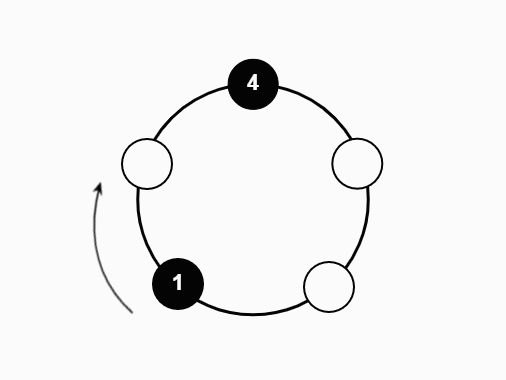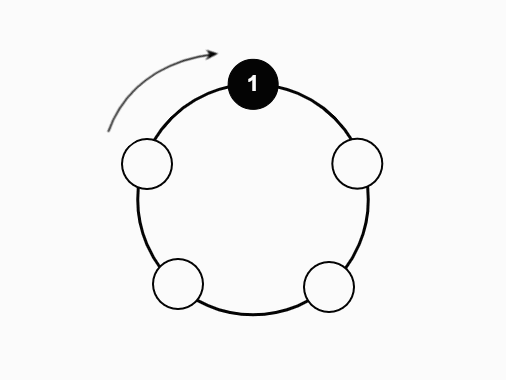
We studied a particle system on the N-cycle under the following process:
- At time t = 0, all vertices on the cycle are occupied by a particle
- At each time step, one particle is sampled uniformly and moved one vertex in the clockwise direction
- If the new vertex is occupied, the particle absorbs the previous occupant
- Repeat until only one particle remains
The central questions we sought to answer were: what can we say about the time before all particles coalesce, and what can we say about the number of steps taken by the last surviving particle? Regarding the first question, we were able to prove an exact formula for the expected time to coalescence as a function of N. For the second, we were able to find a moment-generating function for the steps of the last surviving particle, making it easy to produce formulas for the expectation, second moment, and variance.
We also looked at a similar model on the N-cycle wherein any collision between two particles results in the annihilation of both. This means that for even N, the process concludes when no particles remain, while for odd N the process will leave a single particle alive. We were able to completely describe the even case, getting explicit formulas for the expectation, second moment, and variance.
On the applied side the work involved extensive simulation and multilinear regression on the simulation results, while on the theoretical side we worked with optional stopping and Markov chains conditioned to hit one set before another.